K-Means 클러스터링: 비지도 학습의 대표 알고리즘 🤖
데이터 분석을 진행하다 보면 데이터의 패턴을 찾고 그룹으로 묶는 것이 필요할 때가 많습니다.
비슷한 성향의 고객끼리 묶어줘!
이때 활용할 수 있는 대표적인 비지도 학습 알고리즘이 바로 K-Means 클러스터링입니다.
이번 글에서는 K-Means 클러스터링이 무엇인지, 어떻게 동작하는지, 그리고 실전에서 어떻게 활용할 수 있는지 알아보겠습니다. 📊
비지도 학습(Unsupervised Learning) 복습! 🧠
비지도 학습은 데이터에 정답(라벨)이 주어지지 않은 상태에서 패턴을 찾는 머신러닝 기법입니다.
즉, 학습 데이터에 대한 명확한 출력 값 없이, 알고리즘이 스스로 데이터의 구조를 분석하고 그룹을 찾는 방식입니다. 🤖
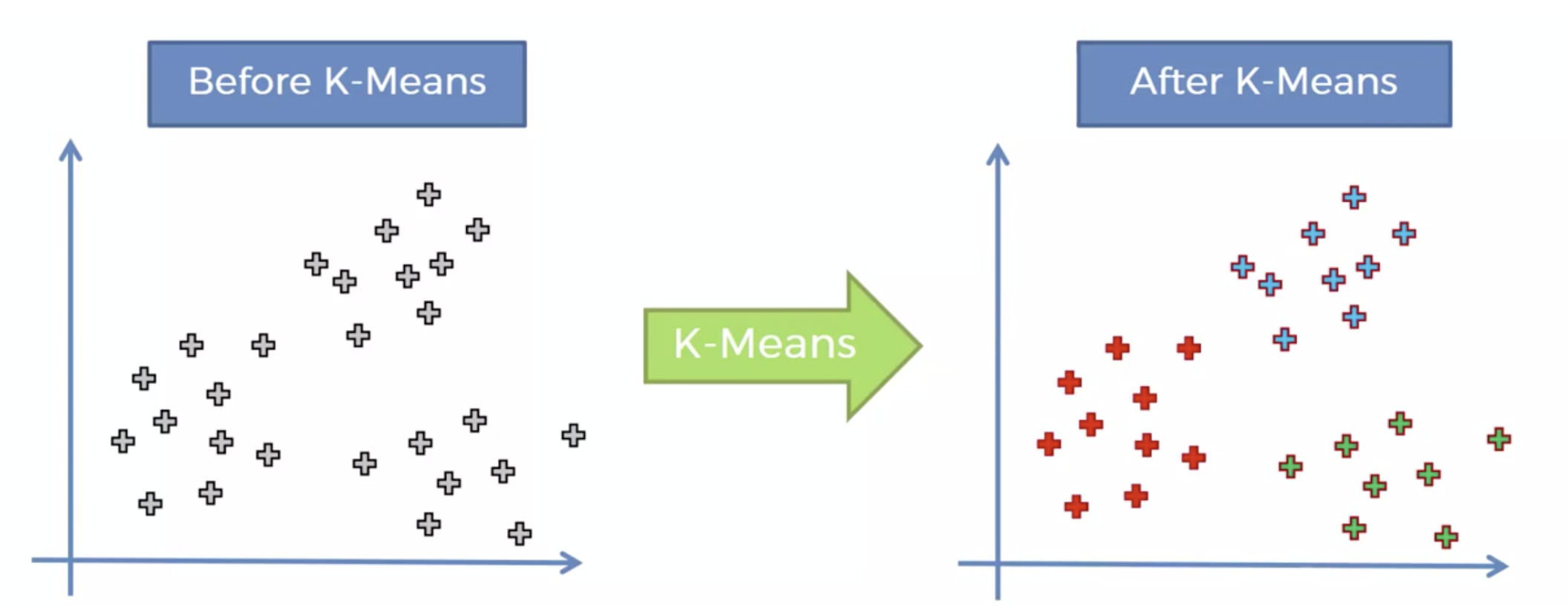
1. K-Means 클러스터링이란? 🧐
K-Means 클러스터링은 주어진 데이터를 K개의 그룹으로 묶는 군집화(Clustering) 기법입니다.
즉, 비슷한 특징을 가진 데이터들을 하나의 그룹으로 분류하는 것입니다.
예를 들어, 고객 데이터를 기반으로 비슷한 소비 패턴을 가진 그룹을 찾거나, 유사한 특성을 가진 제품을 분류하는 데 활용될 수 있습니다. 🔍
2. K-Means 클러스터링의 동작 원리 ⚙️
K-Means 알고리즘은 다음과 같은 과정으로 동작합니다.
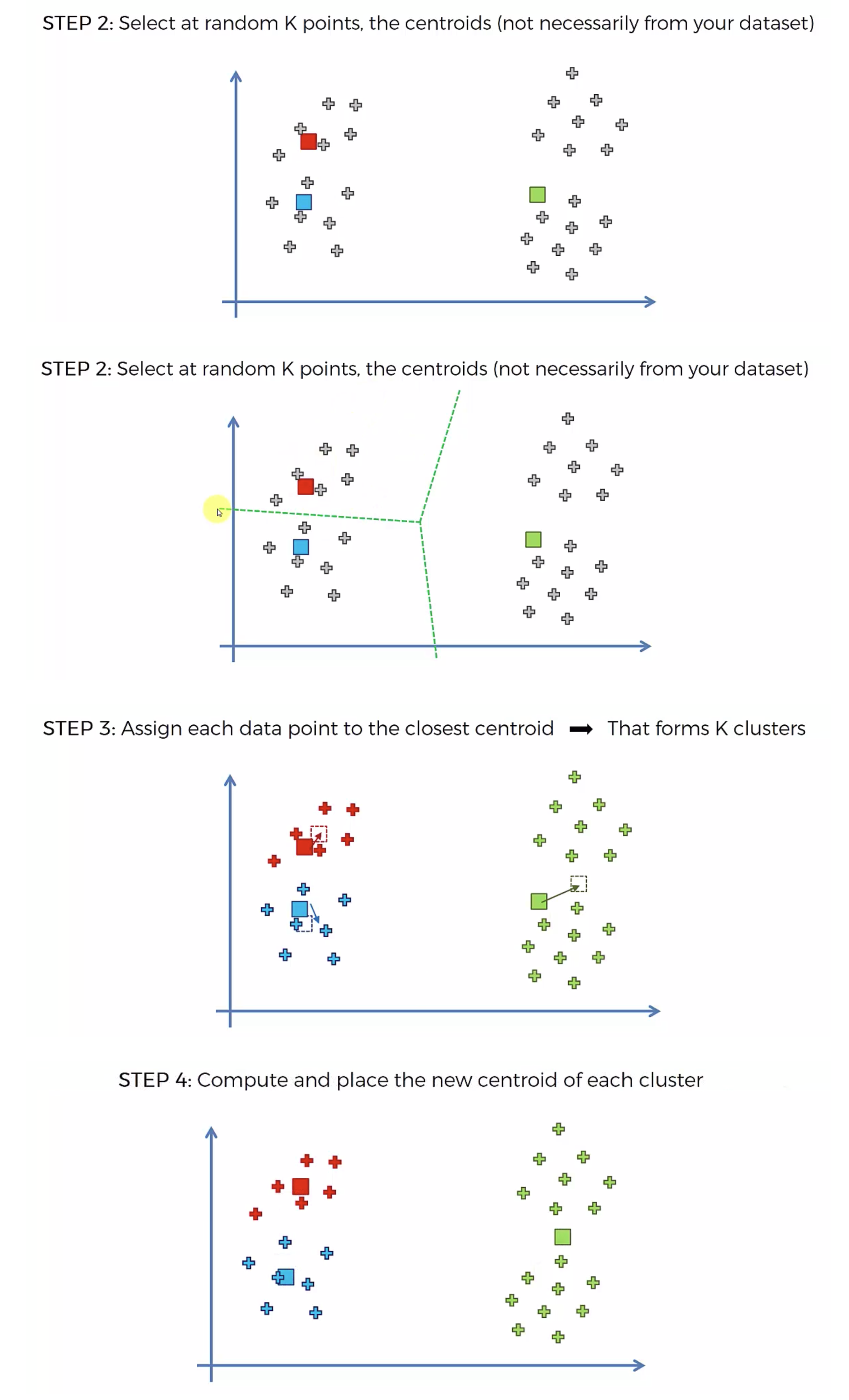
1. 초기 중심점 설정: 원하는 군집 수(K)를 정하고, K개의 초기 중심점(Centroid)을 임의로 설정합니다. 🎯

2. 데이터 할당: 각 데이터를 가장 가까운 중심점에 할당하여 K개의 그룹을 만듭니다. 🏷️

3. 중심점 이동: 각 그룹 내 데이터의 평균을 계산하여 새로운 중심점을 설정합니다. 🔄
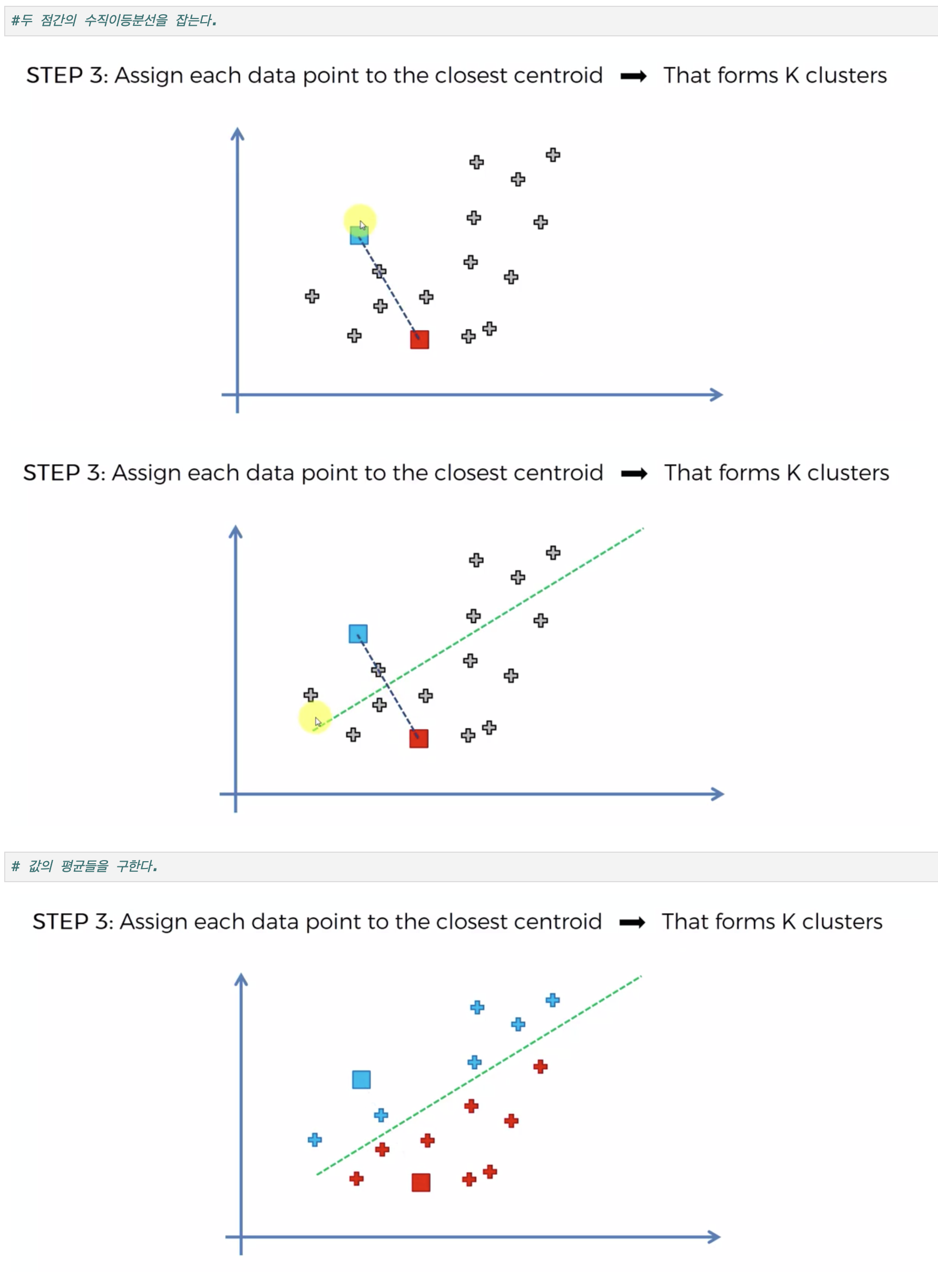
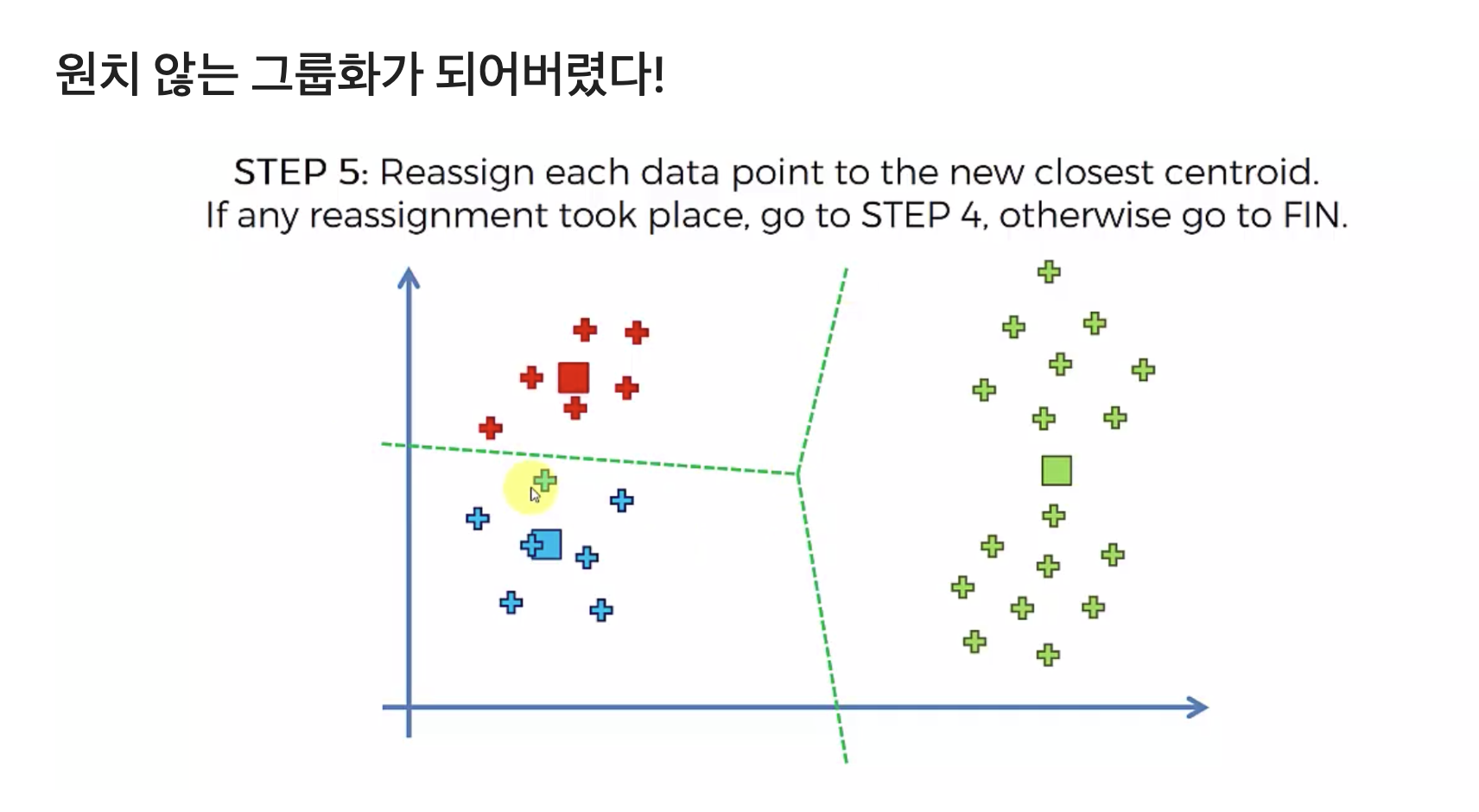
4. 반복 진행: 데이터의 그룹이 더 이상 변경되지 않을 때까지 2~3단계를 반복합니다. 🔁


이 과정을 통해 데이터는 서로 유사한 특성을 가지는 K개의 군집으로 정리됩니다. 📂
3. K-Means의 랜덤 문제와 K-Means++ 🚀
K-Means의 초기 중심점 선택은 랜덤하게 이루어지기 때문에, 실행할 때마다 결과가 다르게 나타날 수 있습니다. 잘못된 초기 중심점을 선택하면 최적의 클러스터를 찾기 어려울 수도 있습니다.
이를 해결하기 위해 K-Means++ 기법이 등장했습니다.
K-Means++의 과정
- 첫 번째 중심점을 데이터 중에서 무작위로 선택합니다.
- 이후 각 데이터와 기존 중심점 간의 거리의 제곱 값을 고려하여 새로운 중심점을 선택합니다. (거리가 먼 점을 우선적으로 선택)
- K개의 중심점이 선택될 때까지 이 과정을 반복합니다.
- 이후 기존 K-Means 알고리즘과 동일한 방식으로 클러스터링을 수행합니다.
이 방법을 사용하면 중심점이 더 균형 잡히게 설정되어 K-Means의 수렴 속도가 빨라지고, 성능이 향상될 수 있습니다. 🔥
4. K값(K-Clusters) 선택 방법 🔢
K값을 정하는 것은 클러스터링에서 중요한 문제입니다.
클러스터의 개수가 너무 적거나, 너무 많으면 차별성이 없어집니다. 그럼 어떻게 최적의 클러스터 개수를 정할 수 있을까요?
일반적으로 **엘보우 방법(Elbow Method)**을 사용합니다.
- 데이터의 K값을 변경하며 클러스터 내 거리(WCSS, Within-Cluster Sum of Squares)를 계산합니다.
- K값이 증가하면 WCSS는 감소하지만, 어느 순간 급격한 감소가 줄어드는 지점이 발생합니다. 📉

- 이 지점을 엘보우 포인트라고 하며, 적절한 K값으로 선택할 수 있습니다. 🏆
5. 실전에서의 활용 🚀
K-Means 클러스터링은 여러 분야에서 활용됩니다.
- 고객 세분화: 쇼핑몰, 금융, 마케팅에서 고객 데이터를 군집화하여 맞춤형 서비스를 제공 🛍️💳
- 이미지 압축: 유사한 색상을 묶어 이미지를 효율적으로 저장 🖼️
- 이상 탐지: 정상 그룹과 비정상 데이터를 구분하여 이상 행동 탐지 ⚠️
6. Python을 이용한 K-Means 구현 예제 🐍
K-Means는 Python의 sklearn 라이브러리를 이용하면 쉽게 구현할 수 있습니다. 아래는 간단한 예제입니다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 데이터 로드
df=pd.read_csv('../data/Mall_Customers.csv')
#빈데이터 체크
df.isna().sum()
#y는 없다. 비슷한 성향으로 묶어달라할 X 데이터프레임만 가져온다.
X=df.loc[ : , 'Genre': ]
#문자열데이터 정리 레이블 인코딩
sorted(X['Genre'].unique())
from sklearn.preprocessing import LabelEncoder
encoder=LabelEncoder()
X['Genre']=encoder.fit_transform(X['Genre'])
#피쳐스케일링은 모델링하며 알아서 적용됨
# K-Means 모델 생성 및 학습
from sklearn.cluster import KMeans
#엘보우 방법으로 클러스터 개수 정하기
wcss = []
for k in range(1, 10+1):
kmeans=KMeans(n_clusters= k, random_state= 31)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot( range(1,10+1) , wcss )
plt.show()
#그래프를 확인하여 클러스터의 개수를 결정 후 학습시킨다.
kmeans=KMeans(n_clusters=6, random_state=31)
y_pred=kmeans.fit_predict(X)
#그루핑한 컬럼을 본래 데이터프레임에 추가하고 확인한다.
df['Group']=y_pred
7. 마무리 🎯
K-Means 클러스터링은 쉽고 강력한 데이터 분석 기법 중 하나입니다.
하지만 이상치(Outlier)에 민감하고, K값을 미리 정해야 한다는 단점도 있습니다.
실무에서는 이러한 단점을 보완하기 위해 DBSCAN, 계층적 클러스터링과 같은 다른 기법과 함께 활용되기도 합니다. 🔄
데이터를 효과적으로 분류하고 분석하는 데 K-Means 클러스터링을 적극 활용해보세요! 🚀
